DEFINISI TURUNAN FUNGSI
TURUNAN FUNGSI
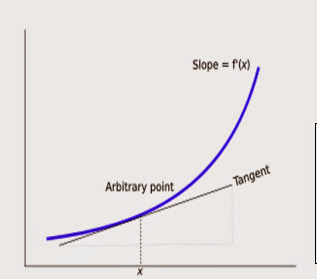
Definisi : Turunan dari suatu fungsi pada titik tertentu menjelaskan sifat-sifat fungsi yang mendekati nilai input. Untuk fungsi yang bernilai real dengan variabel real tunggal, turunan pada sebuah titik sama dengan kemiringan dari garis singgung grafik fungsi pada titik tersebut. Secara umum, turunan suatu fungsi pada sebuah titik menentukan pendekatan linear terbaik fungsi pada titik tersebut.
|
|
Konsep turunan secara fundamental lebih maju dan rumit daripada konsep yang ditemukan di aljabar. Dalam aljabar, seorang murid mempelajari sebuah fungsi dengan input sebuat angka dan output sebuah angka. Tetapi input dari turunan adalah sebuah fungsi dan outputnya juga adalah sebuah fungsi.
Untuk memahami turunan, seorang murid harus mempelajari notasi matematika. Dalam notasi matematika, salah satu simbol yang umumnya dipakai untuk menyatakan turunan dari sebuah fungsi adalah apostrofi. Maka turunan dari f adalah f' (dibaca f aksen).
.
Jika input dari sebuah fungsi adalah waktu, maka turunan dari fungsi itu adalah laju perubahan di mana fungsi tersebut berubah.
Jika fungsi tersebut adalah fungsi linear, maka fungsi tersebut dapat ditulis dengan y=mx+b, di mana:
.
Ini memberikan nilai dari kemiringan suatu garis lurus. Jika sebuah fungsi bukanlah garis lurus, maka perubahan y dibagi terhadap perubahan x bervariasi, dan kita dapat menggunakan kalkulus untuk menentukan nilai pada titik tertentu. Kemiringan dari suatu fungsi dapat diekspresikan:
di mana koordinat dari titik pertama adalah (x, f(x)) dan h adalah jarak horizontal antara dua titik.
Untuk menentukan kemiringan dari sebuat kurva, kita menggunakan limit :
Garis singgung sebagai limit dari garis sekan. Turunan dari kurva f′(x) di suatu titik adalah kemiringan dari garis singgung terhadap kurva di titik tersebut. Kemiringan ini ditentukan dengan memakai nilai limit dari kemiringan garis sekan.
Sebagai contoh, untuk menemukan gradien dari fungsi f(x) = x2 pada titik (3,9):
2. Rumus Dasar Turunan :
a. y = Xn turunannya y' = nXn-1
Contoh : y = 10x3 + 8x2 - x – 3 y' = 30x2 + 16x -1
y = 1/x2 = x -2 y' = -2x -3 = -2/x3
y = x = x1/2 y' = ½ x -1/2 = 1/2x
b. y = c, dengan c adalah konstanta turunannya y' = 0
Contoh : y = 5 y' = 0
c. y sebagai fungsi trigonometri :
y = sin x turunannya y' = cos x
y = cos x turunannya y' = -sin x
y = tg x turunannya y' = sec2x
y = ctg x turunannya y' = -cosec2x
y = secx turunannya y' = secx tgx
y = cosecx turunannya y' = -cosecx ctg x
Contoh : y = -3tgx y' = -3sec2x
y = ctg2x y' = -2cosec2 2x
y = sec2x y' = 2sec2x tg2x
y = cosec3x y' = -3cosec3x ctg3x
y = cos(1-x2) y' = 2xsin(1-x2)
d. y sebagai fungsi logaritma :
y = ln x turunannya y' = 1/x
y = glogx turunannya y' = 1/xlng
Contoh : y = 3logx 1 / x ln3
y = ln 2x 1 / 2x
e. y sebagai fungsi eksponen :
y = ax turunannya y' = ax ln a
y = ex turunannya y' = ex
Contoh : y = 2x y'= 2xln 2
y = ex y' = ex
y = x2 – e3x y = 2x – e3x
SOAL LATIHAN
1. Tentukanlah f '(x) fungsi-fungsi berikut ini.
a. f(x) = x2 + x b. f(x) = cos x
c. f(x) = (5x2 – 1) (3x – 2) d. f(x) = cos x sin x
2. Buktikan jika f(x) = x∛x2 maka f'(x) = 5/3 . x∛x2
Pertemuan - 12
TURUNAN FUNGSI (LANJUTAN)
1. Aturan Rantai Untuk Fungsi Tersusun
Untuk fungsi-fungsi yang bentuknya rumit, di mana y adalah fungsi dari u (atau v), u dan v merupakan fungsi dari x, maka turunannya dicari dengan mengembalikannya ke rumus dasar. Cara pengembaliannya adalah sebagai berikut :
1). y = U y' = (U)'
Contoh : a) y = x3 + 2x2 + 4x + 6
=> y' = 3x2 + 4x + 4
b) y = 2 + 4/x + 7x + 16
= 2x2/3 + 4x-1 + 7x1/2
=> y'= 2.2/3x-1/3 – 4x-2 + 7. 1/2x-1/2
= 4 _ - 4 + 7_
3 x2 2x
c) y = = ( x2 + 1 )1/3
=> y' = 1/3 (2x) (x2+1)-2/3
= 2x_____
3
2). y = U V y' = U' V'
Contoh : y = sin 2x + cos 2x
y' = 2cos2x – 2sin2x
Contoh : y = tg3x – ctg23x
y' = 3sec23x + 6cosec23x . ctg23x
dimana : Ctg23x = ctg3x . ctg3x
U = ctg3x , U' = -3cosex23x
V = ctg3x , V' = -3cosex23x
y' = U'V + UV'
= -3cosex23x . ctg3x + ctg3x . -3cosex23x
= -6cosex23x . ctg23x
3). y = U.V y' = U'V + UV'
Contoh : y = ( x2+1 ) ( 3x3–4x )
U = X2+1 , U' = 2x
V = 3x3-4x , V' = 9x2-4
y' = U'V + UV'
= 2x . (3x3-4x) + (x2+1) . (9x2-4)
= 6x4 – 8x2 + (9x4-4x2+9x2-4)
= 15x4 – 3x2 – 4
Contoh : y = x3.2x
U = X3 , U' = 3x2
V = 2x , V' = 2xln2
y' = U'V + UV'
= 3x2 . 2x + x3 . 2xln2
Contoh : y = 3x2.ex.tgx
U = 3x2 , U' = 6x
V = ex , V' = ex
W= tgx , W' = sec2x
Y' = U'VW + UV'W + UVW'
= 6x.ex.tgx + 3x2.ex.tgx + 3x2.ex.sec2x
Contoh : y = ( x2+1 ) ( 3x+4 )3
U = x2+1 , U' = 2x
V = (3x+4)3 , V' = 9(3x+4)2
y' = U'V + UV'
= 2x.(3x+4)3 + (x2+1).9(3x+4)2
= ( 9x2+24x+16 ).(15x2+8x+9)
= 135x4+432x3+513x2+344x+144
Contoh : y = sinx.coshx
U = sin x , U' = cosx
V = coshx , V' = -sinhx
y' = U'V + UV'
= cosx.coshx - sinx.sinhx
Contoh : y = sin2x.tghx
U = sin2x , U' = -sin2x.cos2x
V = tghx , V' = sechx
y' = U'V + UV'
= cos2xsin2x . tghx + sin2xsechx
Dimana : sin2x = sinx . sinx
U = sinx , U' = cosx
V = sinx , V' = cosx
y' = U'V + UV'
= cosx.sinx + sinx.cosx
= cos2x.sin2x
Contoh : y = coshx2 . cosx2
U = coshx2 , U' = -2xsinhx2
V = cosx2 , V' = -2xsinx2
y' = U'V + UV'
= -2xsinhx2.cosx2 - coshx2.2xsinx2
= -2x {(sinhx2.cosx2 + coshx2.2xsinx2)}
Contoh : y = ( 3x2+1 ) ( sec2x )
U = 3x2+1, U' = 6x
V = sec2x , V' = 2sec2xtg2x
y' = U'V + UV'
= (6x).(sec2x) + (3x2+1).(2sec2xtg2x)
= 2sec2x { 3x + (3x2+1).tgx }
Dimana : sec2x = secx.secx
U = secx , U' = secxtgx
V = secx , V' = secxtgx
y' = U'V + UV'
= secxtgx.secx + secx.secxtgx
= sec2xtgx + sec2xtgx
= 2sec2xtgx
4). y = U/V y' = U'V – UV'
V2
Contoh : y = _x2+1_
x+4
U = x2+1 , U' = 2x
V = (x+4)1/2 , V' = ½(x+4)-1/2
y' = U'V – UV' = (2x)(x+4)1/2 – {(x2+1).1/2(x+4)-1/2}
V2 x + 4
= 2x.x+4 – 1 .(x2+1)
2x+4______
x + 4
Contoh : y = x2+1__
x + lnx
U = x2+1 , U' = 2x
V = x + lnx , V' = 1 + 1/x
y' = 2x.(x+lnx) – (x2+1).(1+1/x)
(x + lnx)2
= 2x2+2xlnx – x2+x+1+1/x
x2+2xlnx+lnx2
Contoh : y = tg2x = sin2x
cos2x
U = sin2x , U' = 2cos2x
V = cos2x , V' = -2sin2x
y' = 2cos2x.cos2x – sin2x . -2sin2x
( cos2x )2
= 2 ( cos22x+ sin22x ) = 2 = 2 sec22x
Cos22x cos22x
Dimana : cos22x+ sin22x = 1
1/cos22x = sec22x
5). Aturan Rantai
Jika y = f(x) merupakan suatu fung si tersusun, yaitu y = g(u) dan u = h(x) maka untuk turunannya dicari dengan cara :
dy = dy . du
dx du dx
Contoh : y = 2u4 – 4u2 – 5u dan u = 4x3 + 3x
Maka :
2. Turunan dari Fungsi Invers
Teorema : misal y = f(x) maka x(y) = f-1(y) disebut Fungsi Invers. Turunan dari Fungsi Invers x(y) adalah x'(y) = atau
Teorema : Turunan fungsi f (x) = xr, r rasional adalah :
f(x) = xr => f'(x) = rxr-1
contoh :
Diberikan suatu fungsi f(x) = = (x2 – 2x)2/3, maka
f'(x) =
=
g(x) = cos
g'(x) = =
-
SOAL LATIHAN DAN JAWABAN
Tentukan Turunan dari :
1. f(x) =
2. f(x) =
3. f(x) =
Jawab :
1) f(x) = =
f'(x) =
=
= =
2) f(x) =
f'(x) =
3) f(x) =
f'(x) =
cari dari x3 + y2 + x2 y3=3
di (1,1)
di (1.1)
jika diminta untuk mencari , maka
5 = – 5 , maka = –1 .
Sumber : arisgunaryati.files.wordpress.com


Post a Comment for " DEFINISI TURUNAN FUNGSI"